
Ruben Arslan writes:
I liked the causal quartet you recently posted and wanted to forward a similar homage (in style if not content) Julia Rohrer and I recently made to trailblaze this paper. We had to go to a triple triptych though, so as not to shrink it too much.
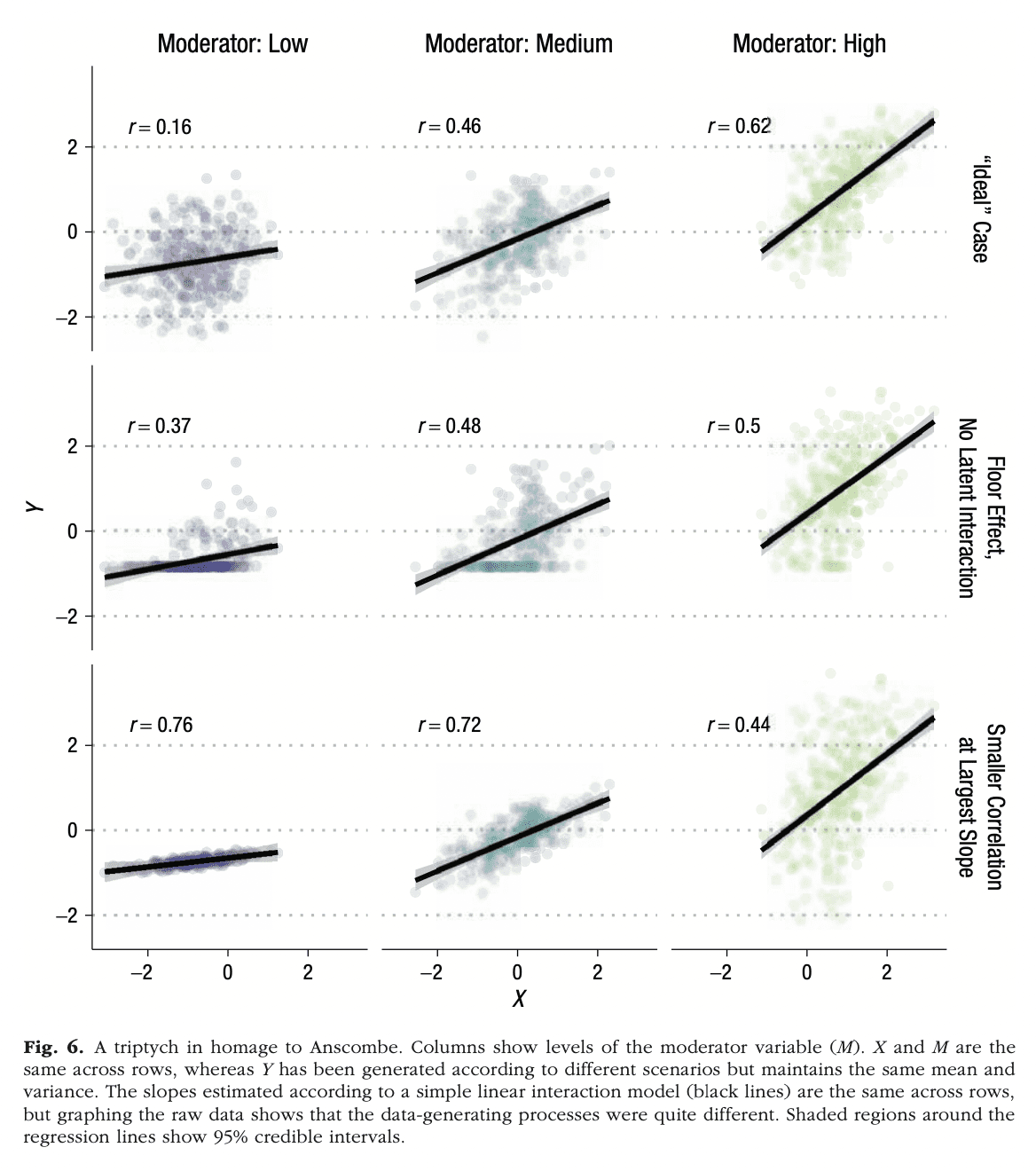
The paper in question is tabbed Precise Answers to Vague Questions: Issues With Interactions.
What to do when a regression coefficient doesn’t make sense? The connection with interactions.
In wing to the tomfool graph, I like Rohrer and Arslan’s paper a lot considering it addresses a very worldwide problem in statistical modeling, a problem I’ve talked well-nigh a lot but which, as far as I can remember, I only wrote up once, on page 200 in Regression and Other Stories, in the middle of installment 12, where it wouldn’t be noticed by anybody.
Here it is:
When you fit a regression to observational data and you get a coefficient that makes no sense, you should be worldly-wise interpret it using interactions.
Here’s my go-to example, from a meta-analysis published in 1999 on the effects of incentives to increase the response rate in sample surveys:
What jumps out here is that big fat coefficient of -6.9 for Gift. The standard error is small, so it’s not an issue of sampling error either. As we wrote in our article:
Not all of the coefficient estimates in Table 1 seem believable. In particular, the unscientific effect for souvenir versus mazuma incentive is very large in the context of the other effects in the table. For example, from Table 1, the expected effect of a postpaid mazuma incentive of $10 in a low-burden survey is 1.4 10(-.34) – 6.9 = -2.1%, unquestionably lowering the response rate.
Ahhhh, that makes no sense! OK, yeah, with some effort you could tell a counterintuitive story where this negative effect could be possible, but there’d be no good reason to believe such a story. As we said:
It is reasonable to suspect that this reflects differences between the studies in the meta-analysis, rather than such a large causal effect of incentive form.
That is, the studies where a souvenir incentive was tried happened to be studies where the incentive was less effective. Each study in this meta-analysis was a randomized experiment, but the treatments were not chosen randomly between studies, so there’s no reason to think that treatment interactions would happen to wastefulness out.
Some lessons from our example
First, if a coefficient makes no sense, don’t just suck it up and winnow it. Instead, think well-nigh what this really means; use the unexpected result as a way to build a largest model.
Second, stave fitting models with rigid priors when fitting models to observational data. There could be a causal effect that you know must be positive—but, in an observational setting, the effect could be tangled with an interaction so that the relevant coefficient is negative.
Third, these problems don’t have to involve sign flipping. That is, plane if a coefficient doesn’t go in the “wrong direction,” it can still be way off. Partly from the familiar problems of forking paths and selection on statistical significance, but moreover from interactions. For example, remember that indoor-coal-heating-and-lifespan analysis? That’s an observational study! (And calling it a “natural experiment” or “regression discontinuity” doesn’t transpiration that.) So the treatment can be tangled in an interaction, plane whispered from issues of selection and variation.
So, yeah, interactions are important, and I think the Rohrer and Arslan paper is a good step forward in thinking well-nigh that.